楕円曲線の一般論に触れつつ、具体例として楕円曲線$y^2=x^3-x$について考察する。
楕円曲線上の加法
まず楕円曲線上の点の加法について復習する。直線と楕円曲線の交点を使った定義もあるが、ここではワイエルシュトラスのペー関数$\wp_{\Lambda}(z)$を使って加法を定義する。
$\C $の格子$\Lambda$に対して
$$\wp_{\Lambda}(z)=\frac{1}{z^2}+\sum_{\omega \in \Lambda}\left(\frac{1}{(z+\omega)^2}-\frac{1}{\omega^2}\right)$$
をワイエルシュトラスのペー関数と呼び、これは二位の楕円関数である。また、アイゼンシュタイン級数
$$G_{2k}(\Lambda)=\sum_{\lambda\in \Lambda\setminus\{0\}}\frac{1}{\lambda^{2k}}$$
に対して、$g_2=60G_4(\Lambda),\,g_3=140G_6(\Lambda)$と定めると、微分方程式
$$\wp'(z)^2=4\wp(z)^3-g_2\wp(z)-g_3$$
を満たす。$P(x,y)=y^2-(4x^3-g_2x-g_3)$とおくと、
$$(\C/\Lambda)\setminus \Lambda \ni [z] \mapsto (\wp(z),\wp'(z))$$
は楕円曲線$P(x,y)=0$への全単射となることが、楕円関数論より分かる。
逆に、このような形の楕円曲線が与えられた時に、対応する格子が存在することが、$j$-不変量などの考察(モジュラー形式の理論)により分かる(従ってペー関数も存在する)。
ここで、楕円曲線上の点の加法を、$P=(\wp(z_1),\wp'(z_1)),Q=(\wp(z_2),\wp'(z_2))$に対して
$$P+Q=(\wp(z_1+z_2),\wp'(z_1+z_2))$$
と定めることにより、楕円曲線にアーベル群の構造を持たせることができる。としたいところであるが、ペー関数は極を持つため、実際は楕円曲線に無限遠点$O$を追加する必要がある。
そこで楕円曲線を射影空間上の代数多様体
$$Y^2Z=4X^3-g_2XZ^2-g_3Z^3$$
と考えることで、$\C/\Lambda$と同型になる。(無限遠点$[1 : 1 : 0 ]$は$\Lambda$に対応する。)
さて、加法が定義できたところで、直線による定義との整合性について述べる。
楕円関数論より、$z_1+z_2+z_3\in \Lambda $のとき
$$\begin {aligned}
\detrix{}{
\wp(z_1)&\wp'(z_1)&1\\
\wp(z_2)&\wp'(z_2)&1\\
\wp(z_3)&\wp'(z_3)&1
}&=0
\end {aligned}$$
であることが分かる(ペー関数の加法公式)。すなわち、$P+Q+R=O$のとき、$P,Q,R$は同一直線上にある。
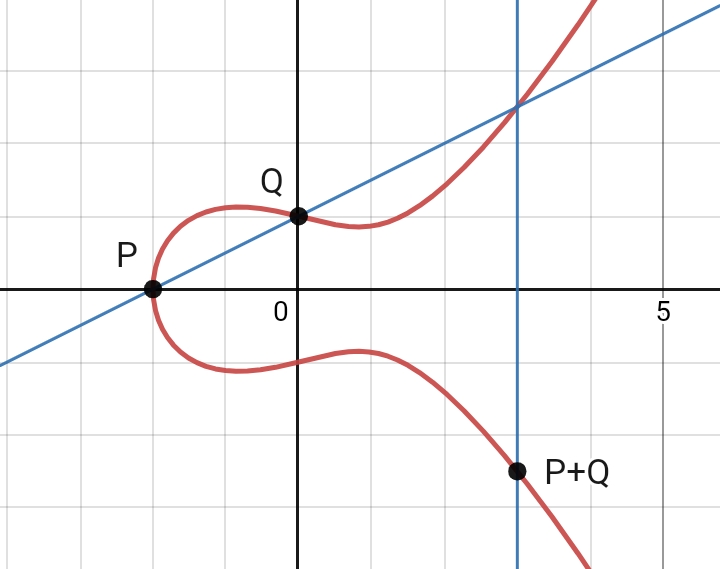
したがって、$P+Q=-R$は、$P,Q$を通る直線と元の楕円曲線の交点のうち$P,Q$でない点の、$y$座標を反転させた点だと説明することもできる。
解と係数の関係から、$P+Q$の座標は$P,Q$の座標の有理関数として書ける。
従って、射影曲線としての楕円曲線$E$に対して、$+:E\times E\to E$は多項式関数であるから、加法は代数多様体の射を定め、$E$はアーベル多様体となる。
楕円曲線の等分点
楕円曲線$E$に対して、$nP=O$となるような点$P\in E$を$E$の$n$等分点と呼び、Eの$n$等分点全体の集合を$E[n]$と表す。
$$\begin {aligned}
E[n]&\simeq (\Lambda/n)/\Lambda\\
&\simeq (\Z^2/n)/(\Z^2)\\
&\simeq (\Z/n\Z)^2
\end {aligned}$$
より$\# E[n]=n^2$である。
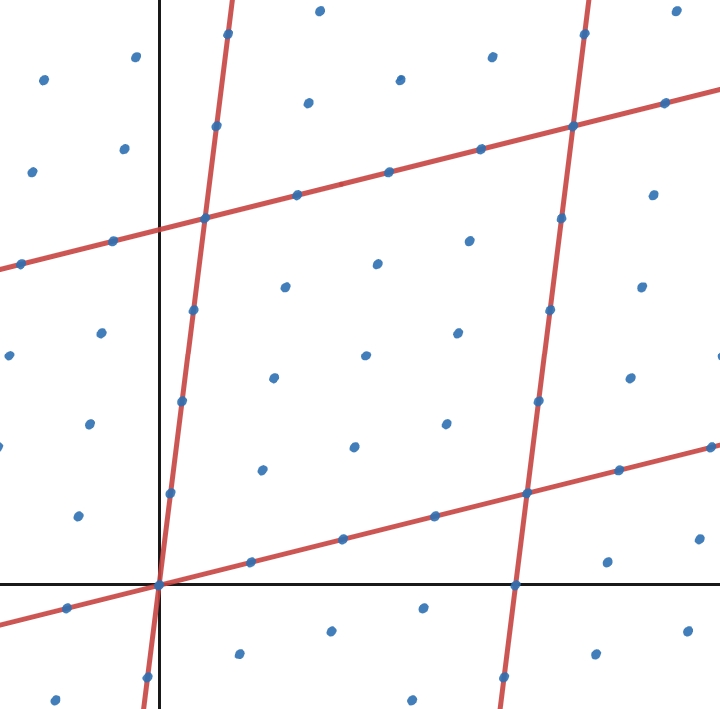
例えば、上の図では、青い点が$4$等分点に対応する複素数を表す($4z\in \Lambda$)。単位格子内には、$16$個の$4$等分点が有ることが分かる。
$E$が有理数係数ならば、$n$等分点の座標は全て代数的数であり、$E[n]$には$G_{\Q}=\Gal(\overline{\Q}/\Q)$が作用する。
さらに、$E[n]\simeq (\Z/n\Z)^2$より、Galois表現$\rho \colon G_{\Q}\to \GL_2(\Z/n\Z)$が得られる。
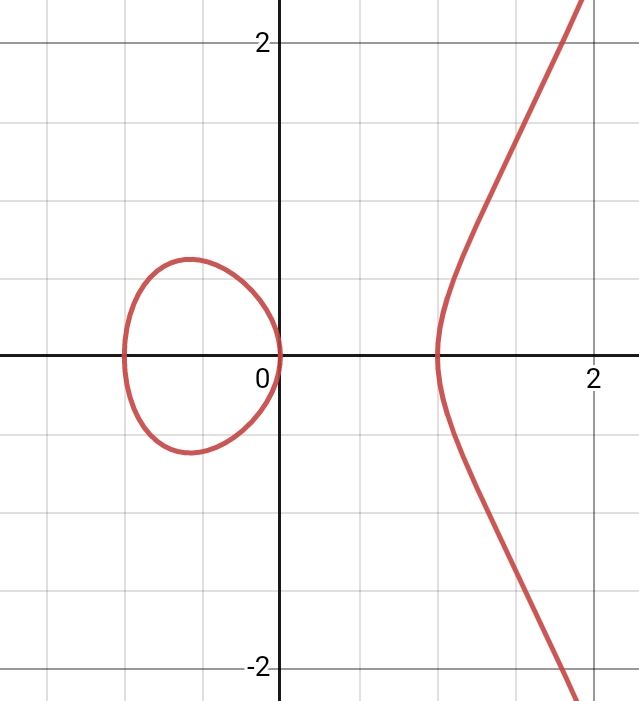
具体例: $y^2=x^3-x$
楕円曲線$E:y^2=x^3-x$を例にとる。グラフは以下の通りである。
加法の計算
$x$座標,$y$座標が異なる$2$点$P(a,b),Q(c,d)\in E$をとり、$P+Q=(e,f)$とする。$P,Q$を通る直線$l$の方程式は
$$\begin {aligned}
y=kx-ka+b
\end {aligned}$$
である。ここで
$$k=\frac{b-d}{a-c}$$
と置いた。従って、$l$と$E$の交点の$x$座標(a,c,e)は、三次方程式
$$\begin {aligned}
\left (kx-ka+b\right )^2=x^3-x
\end {aligned}$$
の三解であり、解と係数の関係から
$$\begin {aligned}
a+c+e&=k^2
\end {aligned}$$
また、$y$座標についても、同様にして三次方程式
$$\begin {aligned}
y^2=\left (\frac {1}{k}y+a-\frac{b}k\right )^3-\left (\frac {1}{k}y+a-\frac{b}k\right )
\end {aligned}$$
が得られるので、解と係数の関係から
$$\begin {aligned}
b+d-f&=-3(ak-b)+k^3
\end {aligned}$$
となる。従って
$$\begin {aligned}
P+Q&=
\left (
-a-c+ k^2,\,
b+d+3(ak-b)-k^3
\right )\\
&=
\left (
-a-c+\left (\frac {b-d}{a-c}\right )^2,\,
b+d-3\frac {ad-bc}{a-c}-\left (\frac {b-d}{a-c}\right )^3
\right )
\end {aligned}$$
と計算できる。ここで$Q\to P$の極限をとると
$$\begin {aligned}
y^2&=x^3-x\\
2y\frac {\d y}{\d x}
&=3x^2-1
\end {aligned}$$
より
$$k=\frac{3a^2-1}{2b}$$
であり、
$$\begin {aligned}
2P
&=
\left (
-2a+ k^2,\,
2b+3(ak-b)-k^3
\right )\\
&=
\left (
-2a+\left (\frac {3a^2-1}{2b}\right )^2,\,
\frac{7}2b+\frac{3a}{b}-\left (\frac {3a^2-1}{2b}\right )^3
\right )
\end {aligned}$$
となり、$2$倍点が得られた。
等分点の計算
今回は、$E$の三等分点を求める。$(x,y)$が三等分点となるのは、先の結果から
$$\begin {aligned}
x&=-2x+\left (\frac {3x^{2}-1}{2y}\right )^2\\
12xy^2&=\left (3x^{2}-1\right )^2\\
12x\left (x^3-x\right )&=9x^4-6x^2+1\\
3x^4-6x^2-1&=0\\
x&=\pm \sqrt {1\pm \frac {2}{\sqrt 3}}
\end {aligned}$$
のときである。$x$の値が$4$つ得られたが、各$x$に対して$y$は$\pm \sqrt{x^3-x}$の二つ存在するので合計$8$個の点が得られ、無限遠点を加えると$9$個の三等分点が得られる。
では、全ての三等分点の座標を計算してみよう。値が複雑になるので
$$A=1+\frac{2}{\sqrt 3},\,B=-1+\frac{2}{\sqrt 3}$$
とおく。
$$\begin {aligned}
P=\left (\sqrt A,\sqrt {2\sqrt {\frac {A}3}}\right ),
Q=\left (-\sqrt {A},i\sqrt {2\sqrt {\frac {A}3}}\right )
\end {aligned}$$
として、残りの点を計算しよう。明らかに
$$\begin {aligned}
2P&=-P=\left (\sqrt A,-\sqrt {2\sqrt {\frac {A}3}}\right )\\
2Q&=-Q=\left (-\sqrt {A},-i\sqrt {2\sqrt {\frac {A}3}}\right )
\end {aligned}$$
である。頑張って計算すると
$$\begin {aligned}
\pm (P+Q)&=\left (-i\sqrt B,\pm (1+i)\sqrt [4]{\frac {B}3}\right )\\
\pm (P-Q)&=\left (i\sqrt {B},\pm (1-i)\sqrt [4]{\frac {B}3}\right )
\end {aligned}$$
となる。しかし、実際に加法の公式を使って計算するとお分かりになると思うが、計算が結構しんどくなる。一方で、計算結果には多くの対称性がある。詳しく説明しよう。
$$\begin {aligned}
A'&=\frac{4A}3=\frac{8}{3\sqrt 3}+\frac {4}3\\
B'&=\frac {4B}{3}=\frac {8}{3\sqrt 3}-\frac {4}3
\end {aligned}$$
とおく。すると
$$\begin {aligned}
P&=\left (\sqrt A,\sqrt[4]{A'}\right )\\
Q&=\left (-\sqrt {A},i\sqrt[4] {A'}\right )\\
-Q&=\left (-\sqrt{A},-i\sqrt[4] {A'}\right )\\
P+Q&=\left (-i\sqrt {B}, \frac {1+i}{\sqrt 2}\sqrt [4]{B'}\right )\\
P-Q&=\left (i\sqrt B,\frac {1-i}{\sqrt 2}\sqrt[4] {B'}\right )
\end {aligned}$$
こう並べると、ガロア群$G_{\Q}=\Gal(\overline{\Q}/\Q)$の作用が露になると思う。例えば、$\sigma\in G_{\Q}$を、複素共役をとる写像とする。すると
$$\sigma(P)=P,\sigma(Q)=-Q$$
であり、実際
$$\sigma(P+Q)=P-Q=\sigma(P)+\sigma(Q)$$
となっている。また、$P,Q$を$E[3]$の基底とすると、$\sigma $の表現行列は
$$\rho(\sigma) = \matrix{}{
1&0\\
0&-1}$$
である。
$$\begin {aligned}
\tr (\rho(\sigma))&=0\\
\det(\rho(\sigma))&=2
\end {aligned}$$
は基底の取り方によらない。(係数は$\Z/3\Z$で考えていることに注意。)
今度は
$$\begin{aligned}
\sigma\left (\sqrt[8]3\right )&=\frac{1+i}{\sqrt 2}\sqrt[8]3\\
\sigma\left (\sqrt[4]{\sqrt 3+2}\right )&=\sqrt[4]{-\sqrt{3}+2}\\
\sigma\left (\sqrt[4]2\right )&=\sqrt[4]2
\end{aligned}$$
とすると
$$\begin {aligned}
\sigma\left (\sqrt {A}\right )&=\sigma \left (\frac {\sqrt {\sqrt 3+2}}{\sqrt [4]3}\right )=\frac {\sqrt {-\sqrt 3+2}}{i\sqrt[4] {3}}=-i\sqrt {B}\\
\sigma\left (\sqrt[4]{A'}\right )
&=\sigma \left (\frac {\sqrt[4]{4\left (\sqrt 3+2\right )}}{3^{8/3}}\right )
=\frac {\sqrt [4]{4\left (-\sqrt 3+2\right )}}{\frac {-1+i}{\sqrt 2}3^{8/3}}
=\frac {-1-i}{\sqrt 2}\sqrt [4]{B'}
\end {aligned}$$
となり、$E[3]$への作用は
$$\begin {aligned}
\sigma \left (P\right )&=2P+2Q\\
\sigma \left (Q\right )&=P+2Q
\end {aligned}$$
である。この表現行列は
$$\rho(\sigma) = \matrix{}{
2&1\\
2&2}$$
であり
$$\begin {aligned}
\tr (\rho(\sigma))&=1\\
\det(\rho(\sigma))&=2
\end {aligned}$$
である。
格子とペー関数
$E$の方程式のままだとペー関数の微分方程式に当てはまらないので、$Y=2y$と置いて、楕円曲線
$$E'\colon Y^2=4x^3-4x$$
を考える。すると$g_2=4,g_3=0$である。
$E'$に対応する格子を$\Lambda =\omega \langle 1,\tau \rangle\quad(\omega>0)$とする。$G_6(i)=0$なので$\tau = i$としてよい。従って
$$\Lambda = \omega \Z[i]$$
である。$\omega$の値は積分により計算することができる。
楕円関数論より、$\wp_{\Lambda }'(z)$の零点は$[\omega/2],[\omega i/2],[\omega (1+i)/2]$であり、それぞれ$(-1,0),(0,0),(1,0) \in E$の何れかに対応している。
$z\in (0,\omega/2]$において$\wp(z)\in R$なので、$(\wp(\omega/2),\wp'(\omega/2))=(1,0)$である。また、この範囲において$\wp'(z)< 0$なので
$$\begin {aligned}
\wp'(z)&=-\sqrt{4\wp(z)^3-4\wp(z)}\\
\d z&=-\frac{\d \wp}{2\sqrt{\wp^3-\wp}}\\
z&=\int _{\wp(z)}^{\infty}\frac {\d x
}{2\sqrt{x^3-x}}\end {aligned}$$
最後の変形において、積分定数は$z\to 0$として決定した。ここで$z=\omega/2$とすると
$$\begin {aligned}
\frac {\omega}2&=\int _1^\infty \frac {\d x}{2\sqrt {x^{3}-x}}\\
&=\frac {1}4\int _{0}^{1}(1-t)^{-1/2}t^{-3/4}\d t\quad \left (t=x^{-2}\right )\\
&=\frac {1}4\frac {\Gamma \left (\frac {1}2\right )\Gamma \left (\frac {1}4\right )}{\Gamma \left (\frac {3}4\right )}\\
&=\frac {\pi ^{3/2}}{2\sqrt 2\Gamma \left (\frac {3}4\right )^2}\\
\omega&=\frac {\pi ^{3/2}}{\sqrt 2\Gamma \left (\frac {3}4\right )^2}
\end {aligned}$$
が得られる。この値を使って少しトリッキーな積分を計算しよう。$z=\omega/3$における値を用いて
$$\begin {aligned}
\frac {\omega}3&=\int _{\sqrt {1+\frac {2}{\sqrt 3}}}^\infty \frac {\d x}{2\sqrt {x^{3}-x}}\\
&=\frac {1}4\int _{0}^{\frac {\sqrt 3}2}(1+t)^{-3/4}t^{-3/4}\d t\quad \left (t=\frac {1}{x^{2}-1}\right )
\end {aligned}$$
より
$$\begin {aligned}\\
\int _{0}^{\frac {\sqrt 3}2}\frac {\d x}{x^{3/4}(1+x)^{3/4}}&=\frac {2\sqrt 2\pi ^{3/2}}{3\Gamma \left (\frac {3}4\right )^2}
\end {aligned}$$
である。いきなりこの積分を与えられても、計算するのは難しいかもしれない。
さらに、関連した級数を計算を計算しよう。
$$\begin {aligned}
\wp'(z)&=-2\sum _{\lambda \in \Lambda}\frac {1}{(z+\lambda)^3}
\end {aligned}$$
だから、$z=\omega/3$を代入して
$$\begin {aligned}
-\sqrt {2\sqrt {\frac {1}3\left (1+\frac {2}{\sqrt 3}\right )}}
&=-2\sum _{\lambda \in \omega Z[i]}\frac {1}{(\omega/3+\lambda)^3}\\
\sum _{\lambda \in \Z[i]}\frac {1}{(1+3\lambda)^3}
&=\frac {\omega^3}{2\cdot 3^3}\sqrt {2\sqrt {\frac {2\sqrt 3+4}{6\sqrt 3}}}\\
&=\frac {\pi ^{9/2}\sqrt {1+\sqrt 3}}{2^{5/4}3^{27/8}\Gamma \left (\frac {3}4\right )^6}
\end {aligned}$$
高階微分の値も同様に計算できる。
アイゼンシュタイン級数
$\omega$が求まったことで、アイゼンシュタイン級数の特殊値が計算できる。$g_2=4$だったので
$$4=60G_4(\Lambda)=60\omega^{-4}G_4(i)$$
より
$$G_4(i)=\frac{\omega^4}{15}=\frac{\pi^6}{60\Gamma\left(\frac 34\right)^8}$$
正規化されたアイゼンシュタイン級数については
$$\begin {aligned}
E_4(i)&=\frac {G_4(i)}{2\zeta (4)}\\
&=\frac {3\pi ^{2}}{4\Gamma \left (\frac {3}4\right )^8}
\end {aligned}$$
これはこちらの記事でテータ関数や算術幾何平均・無限積などを駆使して得た、イータ関数の特殊値
$$\begin {aligned}
\eta(i)&=\frac {\sqrt[4] {\pi }}{\sqrt 2\Gamma \left (\frac {3}4\right )}
\end {aligned}$$
と、モジュラー形式の等式
$$\begin {aligned}
\eta(\tau)^{24}&=\frac {E_4(\tau)^3-E_6(\tau)^2}{1728}
\end {aligned}$$
を合わせて得られる結果と一致する。