$$
\gdef\Res #1{\underset{#1}{\mathrm{Res}}}
\gdef\hi{\hat {\pi }}
\gdef\ti{\tilde {\pi }}
$$
$$\begin {aligned}
\int _{0}^{\infty }\frac {\ln (x)\ln (1+x)}{(1+x)(1+x^{2})}dx
&=-\frac {35}{64}\zeta (3)+\frac {\pi ^{3}}{32}-\frac {\pi ^{2}\ln 2}{32}
\\
\int _{0}^{1}\frac {(1-x)\ln (x)\ln (1-x)}{(1+x)(1+x^{2})}dx
&=\frac {7}{64}\zeta (3)-\frac {\pi ^{2}\ln 2}{32}
\end {aligned}$$
対数は\(0 \leq \arg z < 2\pi \)となるようにとる。
$$I:= \int _{0}^{\infty }\frac {\ln (x)\ln (1+x)}{(1+x)(1+x^{2})}dx$$
とおき、これを求める。
$$\begin {aligned}
f(z):=\frac {\log ^{2}(z)\log (1+z)}{(1+z)(1+z^{2})}
\end {aligned}$$
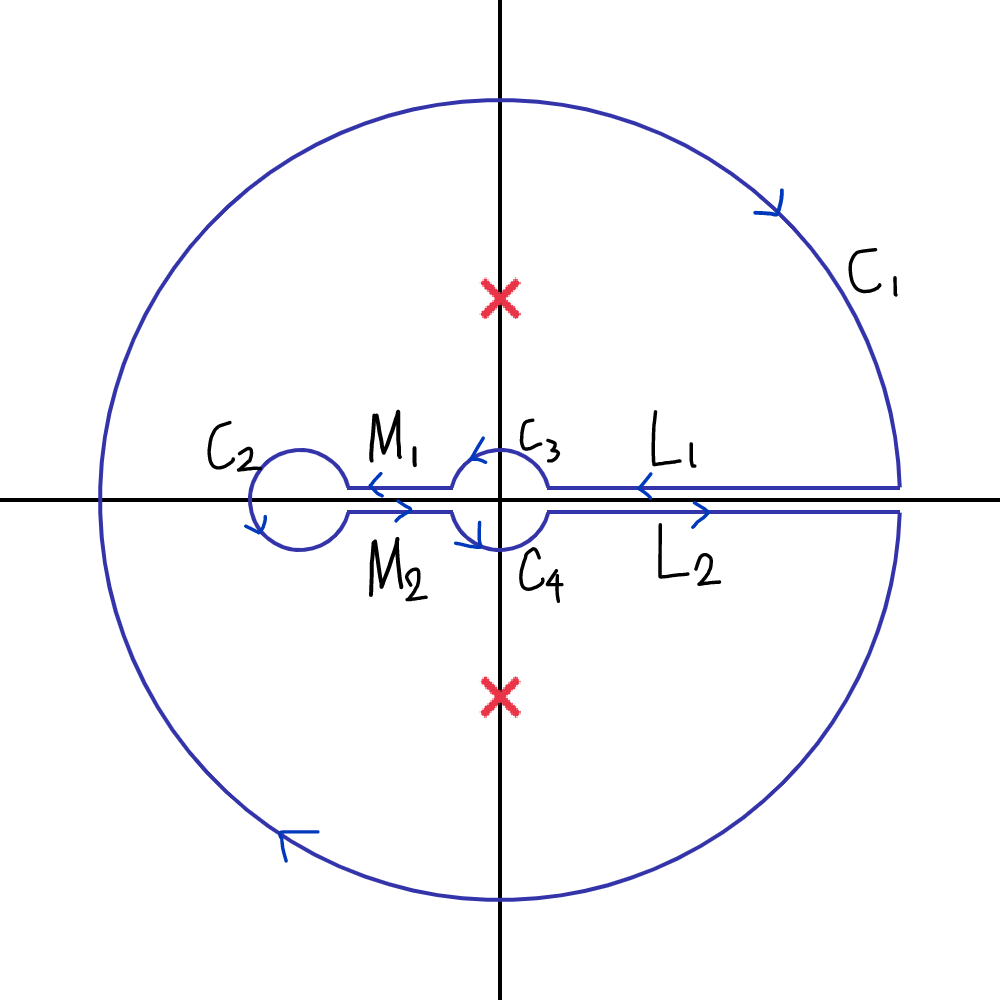
とおく。これを以下の経路で積分する。
$$\begin {aligned}
L_1&:z=x+0i\quad (x:R\to r_1)\\
L_2&:z=x-0i\quad (x:r_1\to R)\\
M_1&:z=x+0i\quad (x:-r_1\to -1+r_2)\\
M_2&:z=x-0i\quad (x:-1+r_2\to -r_12)\\
C_1&:z=Re^{i\theta}\quad (\theta :2\pi \to 0)\\
C_2&:z=-1+r_1e^{i\theta}\quad (\theta:0\to 2\pi)\\
C_3&:z=r_2e^{i\theta}\quad (\theta:0\to \pi)\\
C_4&:z=r_1e^{i\theta}\quad (\theta:\pi \to 2\pi)\\
\\
L&:=L_1+L_2\\
\Gamma &:=M_1+C_2+M_2
\end {aligned}$$
以下、\(R\to \infty,r_2\to 0\)とする。
$$\displaystyle{
\int_{C_1},\int_{C_3},\int_{C_4} = 0
}$$
となるので、留数定理より
$$\begin {aligned}
\int_{\Gamma}+\int_{L}&=-2\pi i\Res{z=\pm i}f(z)\\
\frac 1{2\pi }\Im \left (\int _{\Gamma }+\int _{L}\right )&=-\Re \left (\Res{z=\pm i}f(z)\right ) \quad\quad (33.1)
\end {aligned}$$
となる。(時計回りであることに注意!)
右辺を計算すると、
$$\begin {aligned}
-\Re \left (\Res{z=i}f(z)+\Res{z=-i}f(z)\right )
&=-\Re \left (\frac {\log ^{2}(i)\log (1+i)}{(1+i)2i}-\frac {\log ^{2}(-i)\log (1-i)}{(1-i)2i}\right )\\
&=-\Re\left (\frac {\pi ^{2}}{16}(1+i)\left (\frac {\ln 2}2+\frac {\pi i}4\right )+\frac {9\pi ^{2}}{16}(1-i)\left (\frac {\ln 2}2+\frac {7\pi i}4\right )\right )\\
&=-\left (\frac {\pi ^{2}\log 2}{32}-\frac {\pi ^{3}}{64}+\frac {9\ln 2}{32}+\frac {63\pi ^{3}}{64}\right )\\
&=-\frac {31\pi ^{3}}{32}-\frac {5\pi ^{2}\ln 2}{16} \quad\quad(33.2)
\end {aligned}$$
となる。また、
$$\begin {aligned}
\frac {1}{2\pi }\Im \int _{L}
&=\frac {1}{2\pi }\Im \left (\int _{L_1}+\int _{L_2}\right )\\
&=\frac {1}{2\pi }\Im \int _{L_2}\\
&=\frac {1}{2\pi }\Im\int _{0}^{\infty }\frac {(\ln x+2\pi i)^{2}(\ln (1+x)+2\pi i)}{(1+x)(1+x^{2})}dx\\
&=\frac {1}{2\pi }\int _{0}^{\infty }\Im \frac {(\ln ^{2}x-4\pi ^{2}+4\pi i\ln x)(\ln (1+x)+2\pi i)}{(1+x)(1+x^{2})}dx\\
&=\frac {1}{2\pi }\int _{0}^{\infty }\frac {(\ln ^{2}x-4\pi ^{2})2\pi +4\pi \ln (x)\ln (1+x)}{(1+x)(1+x^2)}dx\\
&=\int _{0}^{\infty }\frac {\ln ^{2}x}{(1+x)(1+x^{2})}dx-4\pi ^{2}\int _{0}^{\infty }\frac {dx}{(1+x)(1+x^{2})}+2I\\
&=\int _{0}^{1}\frac {\ln ^{2}x}{1+x^{2}}dx-4\pi ^{2}\int _{0}^{1}\frac {dx}{1+x^{2}}+2I\\
&=\frac {\pi ^{3}}{16}-\pi ^{3}+2I\\
&=-\frac {15\pi ^{3}}{16}+2I \quad\quad(33.3)
\end {aligned}$$
であり、\(\Gamma\)での積分に関しては、
$$\begin {aligned}
\int _{C_2}f(z)dz&=\int _{C}\left (\frac {\log ^{2}(-1)}{2(1+z)}+O(z)\right )\log (1+z)dz\\
&=\left [-\frac {\pi ^{2}}4\log ^{2}(1+z)\right ]_{-1+r_1e^0}^{-1+r_1e^{2\pi i}}+O(r\ln r)\\
&=-\frac {\pi ^{2}}4\left \{ \left (\ln r+2\pi i\right )^2-\ln ^{2}r\right \} +O(r\ln r)\\
&=-\frac {\pi ^{2}}4\left (4\pi i\ln r-4\pi ^{2}\right )+O(r\ln r)\\
\frac {1}{2\pi }\Im \int _{C_2}&=-\frac {\pi ^2}2\ln r+O(r\ln r)
\end {aligned}$$
$$\begin {aligned}
\frac {1}{2\pi }\Im\int _{M_1+M_2}f(z)dz
&=\frac {1}{2\pi }\Im \int _{0}^{1-r_1}(f(-x-0i)-f(-x+0i))dx\\
&=\frac {1}{2\pi }\Im \int _{0}^{1-r_1}\frac {\log ^{2}(-x)}{(1-x)(1+x^{2})}\left ((\ln (1-x)+2\pi i)-\ln (1-x)\right )dx\\
&=\Re \int _{0}^{1-r_1}\frac {(\ln x+\pi i)^{2}}{(1-x)(1-x^{2})}dx\\
&=\int _{0}^{1-r_1}\frac {\ln ^{2}x}{(1-x)(1+x^{2})}dx-\pi ^{2}\int _{0}^{1-r}\frac {dx}{(1-x)(1+x^{2})}dx
\end {aligned}$$
と変形できる。ここでとの結果
$$\begin{aligned}
\lim _{r\to 0+}\left (\frac {\ln r}2+\int _{0}^{1-r}\frac {dx}{(1-x)(1+x^{2})}\right )
&=\frac {\pi }8+\frac {\ln 2}4
\\
\int _{0}^{1}\frac {\ln ^{2}x}{(1-x)(1+x^{2})}dx
&=\frac {35}{32}\zeta (3)+\frac {\pi ^{3}}{32}
\end{aligned}$$
を用いて、
$$\begin {aligned}
\frac {1}{2\pi }\Im\int _{\Gamma }
&=\frac {1}{2\pi }\Im \int _{M_1+M_2}+\frac {1}{2\pi }\Im \int _{C_2}\\
&=\int _{0}^{1-r}\frac {\ln ^{2}x}{(1-x)(1+x^{2})}dx-\pi ^{2}\int _{0}^{1-r}\frac {dx}{(1-x)(1+x^{2})}-\frac {\pi ^{2}}2\ln r+O(r\ln r)\\
&\xrightarrow{r\to 0}\int _{0}^{1}\frac {\ln ^{2}x}{(1-x)(1+x^{2})}dx-\pi ^{2}\left (\frac {\pi }8+\frac {\ln 2}4\right )\\
&=\frac {35}{32}\zeta (3)+\frac {\pi ^{3}}{32}-\frac {\pi ^{3}}8-\frac {\pi ^{2}\ln 2}4 \\
&=\frac {35}{32}\zeta (3)-\frac {3\pi ^{2}}{32}-\frac {\pi ^{2}\ln 2}4 \quad\quad(33.4)
\end {aligned}$$
が分かるので、\((33.1)\)に\((33.2),(33.3),(33.4)\)を代入して
$$\begin {aligned}
\frac {35}{32}\zeta (3)-\frac {3\pi ^{3}}{32}-\frac {\pi ^{2}\ln 2}4-\frac {15\pi ^{3}}{16}+2I
&=-\frac {31\pi ^{3}}{32}-\frac {5\pi ^{2}\ln 2}{16}\\
2I&=-\frac {35}{32}\zeta (3)+\frac {\pi ^{3}}{16}-\frac {\pi ^{2}\ln 2}{16}\\
I&=\textcolor{blue}{-\frac {35}{64}\zeta (3)+\frac {\pi ^{3}}{32}-\frac {\pi ^{2}\ln 2}{32}}.
\end {aligned}$$